Teorema de Pitágoras
El teorema de Pitágoras únicamente se aplica a triángulos rectángulos y nos relaciona entre sí los tres lados de dichos triángulos. Si utilizamos la siguiente terminología para los lados del triángulo:
Es decir: a es el lado más largo de los tres, opuesto al ángulo de 90º y llamado hipotenusa y b y c son los otros lados, siempre cada uno de ellos más corto que la hipotenusa y llamados catetos. Entonces el teorema de Pitágoras se enuncia como:
Sin embargo, en cualquier problema deberemos despejar alguna de las letras. Si despejamos la hipotenusa obtendremos:
(Aunque siempre que despejamos una raíz debemos tener en cuenta que también podría ser negativa, en este caso el signo menos no tiene sentido ya que estamos hablando de lo que miden los lados de un triángulo, que siempre los tomaremos positivos).
Si lo que queremos es despejar alguno de los catetos:
Notar que en el caso de los catetos tenemos una resta en el interior de la raíz. Para realizar cualquiera de estos cálculos primero calcularemos los cuadrados, luego haremos la suma o la resta y por último la raíz cuadrada.
Aplicaciones del Teorema de Pitágoras
El teorema de Pitágoras puede servir para calcular la diagonal de un cuadrado o rectángulo, sabiendo el resto de lados. Por ejemplo. Sabiendo que un cuadrado tiene 5 cm de lado, hallar la diagonal del cuadrado.
La diagonal del cuadrado es la hipotenusa mientras que los dos catetos miden 5 cm ambos. Aplicando el teorema habiendo despejado la hipotenusa:
El resultado se da en centímetros.
Áreas y perímetros de figuras planas
La primera figura que estudiaremos no es la que tiene menos lados, si no los cuadriláteros, es decir, figuras con cuatro lados.
Empezaremos por los paralelogramos: figuras que tienen los lados paralelos dos a dos.
La más sencilla de todas ellas es la que tiene los cuatro lados iguales y los lados forman ángulos rectos: el cuadrado.
Si el lado del cuadrado mide a, entonces su área es:
y su perímetro es la suma de todos sus lados. Nuevamente si el cuadrado tiene como lado a, el perímetro será: 4a. La diagonal, tal y como vimos en el ejemplo del teorema de Pitágoras, tendrá una longitud de:
La siguiente figura en complicación sería el rectángulo. Un rectángulo es un paralelogramo con lados diferentes dos a dos y ángulos rectos.
El siguiente paralelogramo sería el rombo: en esta figura los ángulos ya no son rectos aunque todos sus lados son iguales.
El rombo tiene como área:
En este caso lo que se utilizan son las dos diagonales, y no los lados. La demostración es sencilla si completamos un rectángulo a partir del rombo de la siguiente manera:
Vemos que el cuadrado del rombo es la mitad del área de un rectángulo de lados D y d.
Si el lado del rombo es a, el perímetro es 4a. La relación entre a y las diagonales es, según el teorema de Pitágoras:
El último de los paralelogramos sería el romboide, cuyos ángulos no son rectos y tiene lados diferentes dos a dos.
El área es la misma que la del rectángulo. A=b·h (Base por altura). Es fácil verlo, pues si recortamos el triángulo de la izquierda y lo colocamos a la derecha obtendremos un rectángulo de base la del romboide y altura, también la del romboide.
El perímetro será la suma de todos los lados: p=2a+2b
Hasta aquí los paralelogramos; los siguientes cuadriláteros ya no tendrán los lados paralelos dos a dos. La siguiente figura que estudiaremos, por tanto, será el trapecio. El trapecio tiene dos lados paralelos, pero los otros dos no. Existen 3 tipos de trapecios: el rectángulo (que tiene un águlo recto)
El trapecio isósceles (que tiene dos lados iguales):
y finalmente el trapecio escaleno (cuyos lados son todos diferentes):
El área del trapecio es:
Esta fórmula es válida para todos los tipos de trapecios.
El perímetro seguirá siendo la suma de todos sus lados. En cada caso deberemos hallar aquellos lados que no nos hallan dado utilizando el teorema de Pitágoras.
Finalmente el último cuadrilátero es el que no tiene ningún lado paralelo: el trapezoide.
Éste es con mucho el más complicado, aunque siempre podríamos descomponerlo en figuras más sencillas: triángulos, trapecios...
Triángulos
Clasificación de los triángulos. Existen diferentes criterios de clasificación de los triángulos. Según sus lados los clasificamos en equiláteros (3 lados iguales), isósceles (dos lados iguales y uno diferente), y escaleno (tres lados diferentes).
He intercambiado el orden en la explicación y he dejado el triángulo para después de los cuadriláteros ya que, conocida el área de un cuadrilátero, es muy sencillo ver que el triángulo tendrá un área la mitad que éste.
Área de un polígono regular
Ahora vamos a ver el área de un polígono regular de más de 4 lados, es decir de pentágonos, hexágonos, heptágonos...regulares.
Pongamos el pentágono como ejemplo:
Los 5 triángulos isósceles tienen la misma área, a saber:
(Perímetro por apotema entre 2).
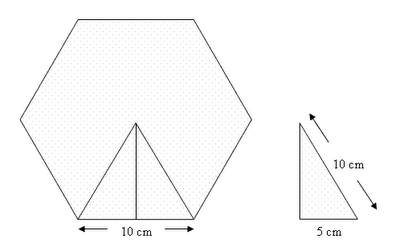
Vamos a ver un caso especial, el del hexágono. Resulta que en el hexágono el radio y el lado tienen la misma longitud, ya que los triángulos en que se descompone el hexágono no son isósceles, si no equiláteros. Esto es fácil de ver si tenemos en cuenta que si dividimos 360º entre 6 nos da 60º, dado que los otros dos ángulos sabemos que tienen que ser iguales, vemos que los 3 valen 60º (para que sumen 180º) por lo que el triángulo es equilátero. Sabiendo ésto, al resolver un problema no será necesario que nos den el valor del radio y del lado, solo nos darán uno de ellos. Además, a partir de éste, la apotema quedará fijada por el teorema de Pitágoras. Por ejemplo, halla el área de un hexágono de lado 10 cm.
Sabiendo que el radio tendrá que medir también 10 cm, podemos calcular la apotema aplicando el teorema de Pitágoras:
Una vez conocida la apotema podemos calcular el área del hexágono:
En el siguiente vídeo podéis ver el mismo ejercicio resuelto, por si todavía quedaba alguna duda:



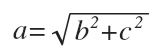




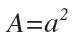

























No hay comentarios:
Publicar un comentario