Este año vamos a estudiar el Teorema del Resto, la potencia de un binomio y las operaciones entre fracciones algebraicas.
Teorema del Resto.
Este teorema relaciona la división entre polinomios y el valor numérico de un polinomio. Dado un polinomio, si lo dividimos por (x-a), obtendremos un resto R. Si a continuación hallamos el valor numérico para x=a, veremos que coincidirá con el resto de la división anterior.
Pongamos un ejemplo. Dado el polinomio:
Vemos que este coincide con el resto de la división.
En el siguiente vídeo, además de la explicación del Teorema del Resto, podrás ver una aplicación del mismo.
Potencia de un binomio.
Hasta ahora hemos aprendido las identidades notables en las que el binomio está elevado al cuadrado, pero ahora vamos a estudiar otras potencias. Para ello, primero vamos a ver como se obtiene el Triángulo de Tartaglia que nos será de utilidad posteriormente.
Cada línea horizontal se obtiene sumando los dos números que están inmediatamente por encima, y en los extremos siempre pondremos unos. Cada línea horizontal se usará en la potencia correspondiente. Por ejemplo, si buscamos una potencia cuarta, utilizaremos la quinta línea (ya que el primer 1 corresponde a la potencia cero). Pongamos un ejemplo.
Para buscar el desarrollo de esta potencia usaremos la línea de números: 1,4,6,4,1 que serán los coeficientes que multiplicarán a las potencias de x y 2. En el primer término tendremos el primer coeficiente, el 1, multiplicando a x elevado al máximo exponente posible: 4, y 2 elevado al mínimo posible: 0. El siguiente término tendrá 4 como coeficiente y x elevado a un exponente una unidad menor que antes, es decir, 3, y 2 elevado a un exponente una unidad mayor, es decir, 1. Y así sucesivamente.
Ahora solo quedaría acabar de hacer los cálculos que fueran necesarios.
En caso de que se tratara de la potencia de una resta, los signos se irían alternado, empezando con el signo positivo. Por ejemplo:
El siguiente vídeo puede acabar de aclarar tus dudas.
Para buscar el desarrollo de esta potencia usaremos la línea de números: 1,4,6,4,1 que serán los coeficientes que multiplicarán a las potencias de x y 2. En el primer término tendremos el primer coeficiente, el 1, multiplicando a x elevado al máximo exponente posible: 4, y 2 elevado al mínimo posible: 0. El siguiente término tendrá 4 como coeficiente y x elevado a un exponente una unidad menor que antes, es decir, 3, y 2 elevado a un exponente una unidad mayor, es decir, 1. Y así sucesivamente.
Ahora solo quedaría acabar de hacer los cálculos que fueran necesarios.
En caso de que se tratara de la potencia de una resta, los signos se irían alternado, empezando con el signo positivo. Por ejemplo:
El siguiente vídeo puede acabar de aclarar tus dudas.
Operaciones con fracciones algebraicas.
Una fracción algebraica es un cociente de polinomios. El año pasado ya vimos cómo simplificarlas. Ahora vamos a operarlas entre sí.
El producto y el cociente es muy sencillo ya que solo interviene el producto de polinomios, pero la suma o la resta, es un poco más complicada, pues debemos hallar el m.c.m. de polinomios. Para ello procedemos igual que cuando sumamos o restamos fracciones numéricas. Se empieza factorizando los denominadores, para poder hallar luego el m.c.m. de los mismos. En este caso factorizamos los polinomios de los denominadores con el mismo propósito. Pongamos un ejemplo:
Seguidamente buscamos el m.c.m. de los denominadores, es decir, los factores comunes y no comunes elevados al máximo exponente. En este caso el m.c.m. será: (x+1)(x-1)(x-1). Este m.c.m. se colocará en los denominadores de ambas fracciones y en el numerador añadiremos los factores por los que hemos multiplicado el denominador (tal y como hacíamos con las fracciones numéricas).
Finalmente solo tenemos que sumar los numeradores y dejamos el denominador común.
Finalmente solo tenemos que sumar los numeradores y dejamos el denominador común.
A continuación os dejo un vídeo en el que puede verse otro ejemplo.
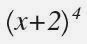
No hay comentarios:
Publicar un comentario