Para este tema es necesario dominar el teorema de Pitágoras, las razones trigonométricas, los sistemas de ecuaciones...También es necesario conocer el sistema de coordenadas cartesiano.
Sistema de coordenadas
A partir de ahora tanto en este tema como en los de funciones, nos referiremos siempre a un sistema de coordenadas cartesiano:
Sobre este sistema de coordenadas representaremos los puntos, los vectores, las rectas y todo tipo de curvas y formas geométricas. Sin embargo, dado que se trata de geometría analítica, siempre resolveremos los ejercicios mediante ecuaciones y dando resultados numéricos cuando sea necesario.
Vectores
Un vector es un segmento orientado (es decir, una flecha). El vector tiene su origen en un punto que llamaremos P, y extremo en otro punto que llamaremos Q.
Las componentes del vector v pueden hallarse a partir de las coordenadas de los puntos P y Q de la siguiente manera:
Siendo P=(p1,p2) y Q=(q1,q2)
Por ejemplo. Halla las componentes del vector que tiene como origen el punto P=(2,1) y extremo el punto Q=(0,-1).
Llamaremos coordenadas a los números que identifican al punto y componentes a las que identifican al vector (aunque en ocasiones se utiliza también el nombre de coordenadas).
Un vector viene caracterizado por: módulo, dirección, sentido y punto de aplicación. El módulo se refiere al tamaño del vector, lo que mide.
Módulo de un vector. A continuación vamos a explicar cómo calcular el módulo de un vector dadas sus componentes. Supongamos que nuestro vector tiene como origen (punto de aplicación) el origen de coordenadas. En esta situación el vector quedaría como sigue:
En este caso está claro que el módulo del vector será la hipotenusa de un triángulo formado además por un par de catetos que corresponden a las componentes del vector. El cateto horizontal mide 1 que es la primera componente del vector y el cateto vertical mide 2 que es la segunda componente del vector.
Así que, según el teorema de Pitágoras, el módulo del vector será:
En general, aunque el vector no tenga origen en el origen de coordenadas, el módulo del vector se podrá calcular de la misma manera, es decir:
Siendo (a,b) las componentes del vector.
La dirección del vector. La dirección del vector viene dada por la recta que pasaría por encima de él o por cualquier otra que fuera paralela. Un conjunto de rectas paralelas tienen la misma dirección. Nosotros utilizaremos los vectores sobre todo para indicar la dirección de una recta.
El sentido, que viene dado por la punta de la flecha y el punto de aplicación (el origen del vector), no serán tan importantes en nuestros cálculos.
Vector unitario. Un vector se dice que es unitario cuando su módulo es igual a 1. Dado un vector cualquiera lo podemos transformar en unitario si dividimos ambas componentes por el módulo de dicho vector. El nuevo vector así obtenido, tendrá la misma dirección que el inicial, pero su módulo será igual a la unidad. Dado el vector (a,b), podremos asegurar que el siguiente vector tendrá módulo 1, es decir, será unitario:
Pongamos un ejemplo. Dado el vector (3,4) hallar el correspondiente vector unitario. A partir de ahora, cuando haga referencia a un vector lo escribiré en negrita, mientras que si hablo de su módulo lo haré sin negrita.
Es fácil comprobar que el vector así obtenido es unitario:
Operaciones con vectores
Las operaciones con vectores que estudiaremos serán: suma y resta de vectores, producto de un número por un vector, y producto escalar de vectores. No está definida la división entre vectores.
Suma y resta de vectores. Sumar o restar vectores es muy sencillo, basta sumar o restar las primeras componentes entre sí y sumar o restar las segundas componentes entre sí. Pongamos un ejemplo: realiza la suma de los siguientes vectores: u=(2,5); v=(3,-1)Para la resta procederíamos de la misma forma pero restando.
La suma de vectores gráficamente se implementa a través de la regla del paralelogramo.
Producto de un número por un vector. También es muy sencillo multiplicar un número por un vector, basta con multiplicar las dos componentes del vector por dicho número, como si se tratara de aplicar la propiedad distributiva. Pongamos un ejemplo: 3·(2,-1)=(6,-3). El efecto que produce el multiplicar un vector por un número (que en este tema recibe el nombre de escalar) es que el vector cambia su tamaño (a no ser que el escalar sea 1 o -1) y podría aumentar (si es mayor que 1 o menor que -1) o podría disminuir (si es entre -1 y 1). Si multiplicamos por un negativo invertimos el vector (le cambiamos el sentido). Si multiplicamos por 0 nos quedamos sin vector. No existe un vector que sea el (0,0).
Producto escalar. Entre vectores están definidos dos productos diferentes, el producto escalar y el vectorial. La diferencia entre ambos (además de cómo se calculan) es que en el producto escalar obtendremos un número (escalar) como resultado, mientras que en el producto vectorial obtendremos un vector como resultado. En este curso solo estudiaremos el producto escalar.
El producto escalar se define de la siguiente manera:
Es decir, el producto escalar de dos vectores (que lo representaremos siempre con un punto) es el producto de los módulos de los dos vectores multiplicado por el coseno del ángulo que forman ambos vectores.
Está claro que si no conocemos el ángulo entre los vectores esta fórmula no nos servirá para calcular el producto escalar, por lo que necesitamos otro método para calcular el producto escalar. Dadas las componentes de los vectores a multiplicar:
podemos calcular el producto escalar de la siguiente manera:
Pongamos un ejemplo: dados los vectores u=(3,1) y v=(2,-1) hallar el producto escalar de ambos.
Usando la última fórmula, el producto escalar será: u·v=3·2+1·(-1)=6-1=5
Ángulo entre dos vectores. En realidad es el ángulo que forman las direcciones (o rectas) que determinan ambos vectores. Gracias a las dos fórmulas del producto escalar, si las combinamos podemos obtener una manera de calcular el coseno del ángulo que determinan ambos vectores y por tanto el ángulo entre ambos vectores. Esta fórmula será:
Es decir: en el numerador tenemos el producto escalar tal y como acabamos de explicar, utilizando las componentes, mientras que en el denominador aparece el producto de los módulos de los dos vectores, que también se calculan a partir de las componentes.
Pongamos un ejemplo. Calcula el ángulo que forman los vectores u=(3,1) y v=(2,-1)
Dado que son los mismos vectores que hemos usado antes ya tenemos calculado el producto escalar, nos había dado 5. Ahora solo tenemos que calcular el producto de los módulos.
Así que el coseno del ángulo que forman será:
Finalmente, y usando la calculadora, podemos saber el ángulo (es el arccos) y nos da un ángulo de 45º.
Hasta aquí la primera parte del tema. Ahora empezaremos la parte de rectas.
Ecuaciones de la recta.
Sobre los ejes de coordenadas podemos representar gráficamente diferentes formas: rectas, curvas...Sin embargo lo que ahora nos interesa es expresar esas formas mediante ecuaciones, y empezaremos por el caso de las rectas.
Ecuación vectorial de la recta. La primera ecuación que deduciremos y que nos servirá para hallar el resto de ecuaciones es la ecuación vectorial de la recta. Se llama así porque está escrita en forma de vectores. La ecuación vectorial de una recta es:
Donde (x,y) es un punto cualquiera que forme parte de la recta (son las variables), (x1,y1) es un punto concreto que sabemos que pertenece a la recta y (u1,u2) es un vector que tiene la misma dirección que la recta (vector director).
A continuación vamos a ver cómo se deduce esta ecuación. En el siguiente gráfico vemos una recta en la que hemos situado dos puntos. Uno de ellos lo hemos especificado, el (2,4), mientras que el otro es un punto variable (x,y), que podríamos haber situado en cualquier otra posición de la recta. También hemos situado un vector sobre la recta. Se trataría de un vector director (v1,v2).
El hecho es que si unimos los dos puntos mediante un vector que vaya de uno al otro: (x,y)-(2,4)=(x-2,y-4), el vector resultante es por fuerza paralelo al vector director (v1,v2).
Para indicar que dos vectores son paralelos lo único que tenemos que especificar es que son proporcionales, es decir, uno es igual a otro excepto en el tamaño. Así que se pueden igualar pero multiplicando uno de ellos, por ejemplo el vector director, por un número que también es variable y que denominamos parámetro.
Ahora solo nos queda sustituir el punto (2,4) por otro punto cualquiera (x1,y1) que en un momento dado sabremos que es un punto de la recta que deberemos además conocer.
Importante: en un caso concreto (x,y) son las variables y no se sustituyen (en principio), mientras que (x1,y1) y (u1,u2) sí que deberían conocerse y poder ser sustituidos.
Pongamos un ejemplo: Escribir la ecuación vectorial de la recta que pasa por el punto (1,2) y tiene como vector director (3,-1).
Ecuaciones paramétricas. A continuación transformaremos la ecuación vectorial para escribirlas en diferentes formas. Lo primero que haremos será igualar las primeras componentes de un miembro de la igualdad a las primeras del segundo miembro y las segundas componentes a las segundas.
De esta manera hemos obtenido un par de ecuaciones en las que en cada una de ellas aparece el parámetro, y por ello reciben este nombre.
Ecuación continua. Si a continuación despejamos el parámetro de cada ecuación e igualamos lo que queda en el segundo miembro de cada ecuación obtendremos la ecuación continua:
Es importante no perder de vista dónde ha ido a parar el punto y el vector. Pongamos un ejemplo. ¿Cual es el punto y el vector director de la siguiente recta?
El punto es el (3,-1) y el vector director es el (2,-5).
Ecuación general o implícita. Para escribir la siguiente forma lo que haremos es pasar todos los términos a un mismo lado de la igualdad y dejar un 0 al otro lado. Para ello primero pasamos v1 y v2 multiplicando a los otros miembros de la igualdad:
A continuación aplicamos la propiedad distributiva:
Y finalmente pasamos todos los términos al mismo lado:
En un caso concreto, todo serán números excepto x e y, por lo que podemos renombrar aquellos coeficientes y términos que en un caso concreto serán números:
con lo que la ecuación general la escribiremos como:
En estos instantes todavía somos capaces de ver de forma casi inmediata el vector director, pero el punto se pierde completamente de vista. Por ejemplo. Dada la ecuación general: 3x-2y+1=0 da su vector director y un punto que pertenezca a la recta.
Para hallar el vector tenemos que invertir el orden de A y B y cambiarle el signo a B, así que el vector director será: (-B,A)=(2,3). Para hallar un punto de la recta C no nos da directamente el punto, por lo que lo que podemos hacer es algo más sencillo: le damos a x el valor que queramos y buscamos el correspondiente valor de y (tabla de valores). Por ejemplo, si x=0, entonces queda: -2y+1=0 y por tanto y=1/2. Así el punto (0, 1/2) es un punto que pertenece a la recta.
Ecuación explícita. La última forma en la que veremos a la ecuación de la recta (aunque existen más formas) será la ecuación explícita. Para hallarla lo único que tenemos que hacer es despejar la y de la ecuación general:
Ahora solo falta hacer un cambio, nuevamente lo que en un caso concreto sea un número lo podemos llamar de otra manera, así si:
entonces la ecuación explícita quedará:
Esta forma de escribir la ecuación de la recta es la que utilizaremos en el tema de funciones.
¿Qué significado tienen m y n? Tanto m como n tienen dos significados matemáticos importantes. En concreto, m es la pendiente de la recta. Vamos a verlo. Si deshacemos los cambios vemos que m es:
¿Y qué representa este cociente? Veámoslo en el gráfico:
Este cociente es la relación entre lo que se avanza hacia la derecha respecto a lo que se sube. Es decir, la pendiente. Si aumenta v2 aumenta la pendiente, pero si aumenta v1 disminuye la pendiente.
¿Y la n? Si en la ecuación explícita hacemos x=0 nos queda: y=n, es decir, n es la coordenada de corte con el eje y de la recta.
Una vez explicadas todas las formas de la recta lo que podemos hacer es pasar de una forma a otra en un caso concreto. Dada la ecuación (x,y)=(2,-1)+k(-1,3) escribe el resto de formas:
Si quisiéramos pasar directamente de la ecuación vectorial a la ecuación general lo que deberíamos hacer es escribir primero A=v2=3; B=-v1=1 y luego nos quedaría saber el valor de C. Por ahora tendríamos: 3x+y+C=0. Para hallar el valor de C sustituimos x,y por el punto que sabemos que pertenece a la recta que es el (2,-1): 3·2-1+C=0; C=-5. Y ya tendríamos la ecuación general de la recta sin necesidad de pasar por el resto de formas.
Observa el siguiente vídeo en el que se aplica lo estudiado en el apartado: ecuaciones de la recta, para resolver un ejercicio:
Dadas dos rectas, podemos estudiar la posición relativa entre ambas, es decir, como están una respecto a la otra. Puede que sean dos rectas paralelas, que sean la misma recta, que se corten (y en este caso podemos estudiar el punto de corte y el ángulo que forman. También podemos ver en que caso las rectas son perpendiculares.
A partir de ahora vamos a utilizar la ecuación general de la recta.
Rectas coincidentes. Dos rectas: Ax+By+C=0; A'x+B'y+C'=0, son coincidentes, es decir, son iguales, cuando los coeficientes son proporcionales.
Lo que ocurre en este caso es que toda la ecuación ha sido multiplicada por el mismo número obteniendo otra con unos coeficientes diferentes pero todos multiplicados por el mismo número.
Rectas paralelas. Dos rectas: Ax+By+C=0; A'x+B'y+C'=0, son paralelas cuando cumplen:
Es decir, la parte que corresponde al vector director es proporcional, la A y la B, mientras que la que está relacionada además con el punto, la C, ya no es proporcional.
Rectas secantes. En este caso basta tan solo que la parte del vector director no sea proporcional:
En este último caso se puede hallar el punto de corte entre las rectas secantes si resolvemos el sistema entre las dos rectas. También es posible hallar el ángulo que forman las dos rectas utilizando la fórmula del coseno del ángulo que forman las rectas:
Donde debemos conocer los vectores directores de las rectas.
Pongamos un ejemplo. Halla el punto de corte y el ángulo formado entre las rectas: 2x-y+1=0; 3x+y+4=0
Para empezar comprobaremos que son rectas secantes.
A continuación resolveremos el sistema. Sumando las dos ecuaciones eliminamos la y, obteniendo: 5x+5=0; x=-1. Sustituyendo luego el valor de x en cualquiera de las dos ecuaciones: 2(-1)-y+1=0; y=-1. El punto en el que se cortan las rectas es: (-1,-1).
Ahora calcularemos el ángulo que forman. Para ello primero buscaremos los vectores directores de cada recta. Sabiendo que A=u2 y B=-u1 Tenemos los vectores: (1,2) y (-1,3) respectivamente. Usando a continuación la fórmula:
No es necesario utilizar la calculadora para saber que el ángulo es 45º. (Sin embargo, existe otro ángulo entre estas rectas: 180º-45º=135º)
Veamos la representación gráfica del problema: (la recta en rojo es 2x-y+1=0; la recta en azul es 3x+y+4=0)
Observa ahora el siguiente vídeo en el que se explica la posición relativa entre dos rectas y además se resuelve un ejercicio:
Condición de perpendicularidad
La condición para que dos rectas sean perpendiculares viene dada por el ángulo entre los vectores directores. Éste debe ser de 90º y por tanto el producto escalar debe ser 0:
Así que la condición para que dos rectas sean perpendiculares es que el producto escalar de sus vectores directores sea 0.
Según la expresión anterior, para que el producto escalar nos de 0 basta con que las componentes de los vectores estén intercambiadas de orden, y que una de ellas esté cambiada de signo. Es decir (u1,u2) y (u2,-u1) serían perpendiculares, ya que: u1·u2-u1·u2=0 (también podría servir cualquier vector que cumpliera lo anterior pero que además estuviera multiplicado por cualquier número).
Pongamos un ejemplo. ¿Son perpendiculares los siguientes vectores directores: u=(2,1) y v=(-3,6)?
Sí que son perpendiculares ya que: 2·(-3)+1·6=-6+6=0
Apliquemos lo anterior al caso de dos rectas. ¿Son perpendiculares las siguientes rectas: 3x-y+5=0; 2x+6y-8=0?
Busquemos los vectores directores. Para la primera recta es el (1,3), mientras que para la segunda recta es el (-6,2) si ahora hacemos el producto escalar: 1·(-6)+3·2=-6+6=0. Por lo que son perpendiculares.
En el ejemplo anterior, las rectas estaban en su forma general. En este caso, no es necesario buscar los vectores directores, ya que los vectores formados por los coeficientes (A,B) de la ecuación, cumplen la misma condición. (3,-1)·(2,6)=3·2+(-1)·6=6-6=0. ¿Por qué ocurre esto? si nos fijamos bien en estos vectores (A,B) vemos que cumplen por su definición: (A,B)=(v2,-v1), es decir: componentes cambiadas de orden y un signo cambiado. Por lo que los vectores (A,B) que pueden verse en la ecuación general son justamente vectores perpendiculares a la recta. Por eso, para comprobar la perpendicularidad de dos rectas también pueden usarse estos vectores, ya que si son perpendiculares los directores también lo serán éstos.
Veamos la gráfica del ejemplo:
Si dibujamos los vectores (A,B)=(3,-1) y (A',B')=(2,6)) veremos que son vectores perpendiculares a cada una de sus respectivas rectas.
Éste es uno de los ejercicios más interesantes que se pueden plantear.
Como acabamos de explicar, no es necesario trabajar con los vectores directores, si no que podemos utilizar los vectores (A,B). Así el vector (A,B) del ejercicio es el (2,-1). Si queremos tener un vector que sea perpendicular a éste, lo que tenemos que hacer es intercambiar las componentes y cambiar el signo de una de ellas. Así (1,2) es perpendicular al dado (2,-1). Sustituyamos entonces el (1,2) en la ecuación de la recta. Por ahora ya tendremos: x+2y+C=0. Ya conocemos A y B, ahora nos hace falta hallar C. Para ello sustituyamos (x,y) por el punto por el que debe pasar, que es el (0,-2). Así: 0+2·(-2)+C=0; C=4. Con lo que la recta que buscamos será: x+2y+4=0.
Veamos este problema en un gráfico:
También podríamos plantear un problema parecido pero en lugar de buscar la recta perpendicular nos pedirían la recta paralela. Por ejemplo, hallar la recta paralela a 3x-y+2=0, y que pase por el punto (2,1)
En este caso, al buscar una recta paralela, no es necesario cambiar el (A,B): 3x-y+C=0. Ahora solo falta sustituir (x,y) por el punto por el que pasa para poder hallar C: 3·2-1+C=0; C=-5. Así la ecuación de la recta quedará:: 3x-y-5=0.
Observa a continuación el siguiente vídeo en el que se resuelve un ejercicio:
Distancias
Para acabar el tema vamos a ver cómo se calculan las distancias en el plano. Podemos calcular la distancia entre dos puntos, o entre un punto y una recta o entre dos rectas paralelas.
Distancia entre dos puntos. La distancia entre dos puntos se calcula a través del módulo del vector que une los dos puntos. Por ejemplo: halla la distancia entre los puntos P=(2,3) y Q=(1,-2).
Primero hallaremos el vector que va de P a Q (o viceversa): PQ=(1-2,-2-3)=(-1,-5). Seguidamente se calcula el módulo del vector PQ.
Distancia entre punto y recta. En este caso utilizaremos una fórmula (que no demostraremos). La distancia entre un punto P=(x',y') y la recta de ecuación general: Ax+By+C=0 es:
Observa a continuación el siguiente vídeo:
Problemas de aplicación
A continuación vamos a ver algunos ejemplos de aplicación de lo estudiado durante el tema a la resolución de problemas. Empezaremos por algunos casos de lo que se conoce como lugares geométricos. Éstos son puntos del plano que cumplen una determinada propiedad. Entre ellos tenemos: la mediatriz de un segmento o la bisectriz de un ángulo.
Mediatriz de un segmento. La mediatriz de un segmento es la recta que equidista (todos sus puntos tienen la misma distancia) de dos puntos que son los extremos de un segmento. Esta recta lo que hace, en definitiva, es cortar a un segmento por su punto medio de forma perpendicular. Ambas definiciones nos llevan a resolver el problema de dos maneras diferentes. Según la primera definición. echaremos mano de la distancia entre puntos para escribir la ecuación de la mediatriz, mientras que en el segundo caso, lo que se utiliza es la condición de perpendicularidad, para hallar la ecuación de la recta perpendicular a otra y que pasa por un determinado punto (en este caso el punto medio del segmento).
Vamos a explicarlo con un ejemplo. Vamos a hallar la mediatriz del segmento que tiene por extremos los puntos A(-2,3) y B(2,5). Para ello aplicamos la fórmula de la distancia entre puntos:
Hemos igualado la distancia de un punto cualquiera (x,y) a el punto A con la distancia de este mismo punto (x,y) al punto B. A continuación operamos. Primero eliminamos las dos raíces (directamente). Luego desarrollamos los cuadrados de los binomios:
Seguidamente pasamos todos los términos al primer miembro para que quede igualado a cero. Vemos que los cuadrados se nos van y nos queda:
Seguidamente os muestro un vídeo en el que se resuelve el mismo ejercicio pero usando el segundo método:
También podemos aprovechar las definiciones de distancia para calcular áreas de figuras planas. Por ejemplo, para calcular el área de un triángulo a partir de los puntos de sus vértices.
Área de un triángulo. En el siguiente vídeo, además de resolver un problema de este tipo, se repasan varios conceptos más:







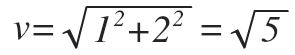



















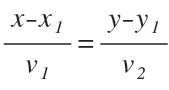





























No hay comentarios:
Publicar un comentario