Antes de empezar el tema deberás dominar el cálculo con potencias, ya que éste se dará por sabido y no se volverá a explicar. Para repasar potencias puedes estudiar el Tema 1: Números Racionales de 3º de ESO donde se estudian las potencias de exponente negativo, y el Tema 1: Números Enteros de 2º de ESO donde se estudian las potencias de números. También deberás dominar el cálculo con fracciones y las identidades notables. La notación científica, relacionada con el cálculo con potencias decimales, deberás repasarla del tema 2: Números Reales de 3º de ESO
Radicales.
Aunque en años anteriores has aprendido a calcular raíces cuadradas, e incluso cúbicas, este año el cálculo con raíces va a ser mucho más importante. Sin embargo, no se tratará de calcular un único número, si no, como ocurría con los cálculos con potencias, lo que nos interesará será operar las raíces entre sí y dejarlas lo más simplificadas posible.
Este año las raíces no serán siempre raíces cuadradas. Así que pueden ser raíces cúbicas, cuartas, quintas...Esto se indica por el índice que, cuando era una raíz cuadrada se omitía y se daba por supuesto. Sin embargo, es importante no olvidarse el índice de la raíz. No es lo mismo una raíz cuadrada que una raíz cúbica. La siguiente sería una raíz de índice n o raíz enésima. El número "a" del que realizamos la raíz se denomina radicando:
El resultado de hacer la raíz da un número "b" tal que si elevamos "b" a "n" nos tiene que dar de nuevo "a".
Por ejemplo:
Dado que los radicales no dejan de ser potencias, aunque de exponente fraccionario:
Todas las propiedades de las potencias también se aplicarán a los radicales. Así podremos tener una serie de propiedades equivalentes aunque expresadas en forma radical. Llegados a este punto tenemos dos opciones, o pasamos los radicales a potencias y hacemos las operaciones con potencias (de exponente fraccionario) dejando luego el resultado nuevamente en forma radical, u operamos los radicales directamente con las propiedades deducidas a continuación. Algunos profesores prefieren la primera opción, aunque si uno aprende a usar las propiedades de los radicales los cálculos son más rápidos. Así que nosotros utilizaremos esta segunda opción.
Simplificación de radicales.
Aunque éste será el último paso que realicemos en las operaciones entre radicales, vamos a empezar por explicar que, dado que índice y exponente se situarían como numerador y denominador en la forma de potencia, pueden simplificarse entre sí si tienen factores comunes. Por ejemplo:
Ha sido posible simplificar el 16 y el 12 dividiéndolos ambos entre 4. De esta forma se obtiene un radical equivalente aunque más simplificado.
Extracción de factores de un radical.
También consideraremos que un radical está más simplificado si podemos extraer de la raíz algunos factores. Para ello lo que tenemos que hacer es dejar siempre el radicando en forma de potencia y si el exponente del radicando es mayor que el índice, entonces siempre será posible extraer algún factor. Veamos un ejemplo:
Lo que hemos hecho es descomponer la potencia del radicando en dos potencias (cuyos exponentes suman 7, por la propiedad del producto de potencias de la misma base) tal que una de ellas tiene el mismo exponente que el índice del radical. Así, ese exponente se simplifica tal y como hemos visto antes con el índice y queda 5/5=1 como exponente del 3 que ya ha quedado fuera de la raíz. La otra potencia no puede simplificarse y se mantiene en el interior.
Veamos otro ejemplo:
En este caso, dado que 12 incluye 2 veces el 5, ya hemos descompuesto el 12 en un múltiplo de 5, como es el 10 y luego el 2 que sobra. Luego simplificamos 10/5=2 que es el exponente del 3 que ha salido fuera de la raíz.
Reducción a índice común.
Dado que el índice se corresponde con el denominador de la forma potencial, cuando tengamos que multiplicar raíces, en realidad estaremos sumando fracciones, y las fracciones para sumarse necesitan común denominador, por lo que es muy recomendable saber poner índice común.
El sistema también será el mismo que cuando ponemos común denominador. Calculamos el m.c.m. de los índices, y luego multiplicamos los exponentes de los radicandos por los factores que hayamos multiplicado los índices. Pongamos un ejemplo:
Primero buscamos el mínimo común múltiplo de 6 y 15. m.c.m.(6,15)=2·3·5=30. Luego, para saber por qué número multiplicaremos el exponente del radicando dividimos el m.c.m. entre cada índice: 30:6=5; 30:15=2. Así nos queda:
Suma y resta de radicales
Una vez más, la suma y la resta no va a ser tan fácil que se pueda hacer que el producto y la división, dado que, como ocurre con las potencias, solo podremos sumar o restarlas si son idénticas, en cuyo caso se podrán sacar factor común y sumaríamos o restaríamos solo los coeficientes. Pongamos un ejemplo:
Si no tuviéramos la misma raíz intentaríamos arreglarlas para que fueran iguales, pero si no fuera posible no podríamos realizar la suma o resta. Por ejemplo:
Lo primero que deberemos hacer es descomponer los radicandos en factores primos.
Según lo que hemos visto con la simplificación de radicales podemos extraer algunos factores de las raíces:
En la segunda raíz además hemos simplificado el índice con el exponente del radicando. Ahora ya podemos sumar, pero solo las dos primeras:
La última raíz al ser diferente no podrá sumarse a las anteriores y se dejará tal cual.
Producto y división de radicales
El producto y la división siempre se podrán realizar. Solo será necesario que las raíces tengan el mismo índice. Una vez que tengan todas el mismo índice y hallamos multiplicado los exponentes por el factor necesario, podremos realizar el producto. Para ello solo tendremos que unir los radicandos bajo la misma raíz.
Pongamos un ejemplo:
No hemos realizado la operación del radicando ya que el resultado es un número muy grande y no viene al caso, pero si no ya podríamos operarlo.
Potencia de un radical y radical de radical.
La potencia de un radical se calcula fácilmente ya que es como la potencia de una potencia, solo será necesario elevar el exponente del radicando. Por ejemplo:
En el caso de radical de radical ocurre lo mismo, se multiplican los índices. Por ejemplo:
Racionalización.
La racionalización es la operación que consiste en eliminar las raíces del denominador en una fracción.
Distinguimos 3 casos básicos (los hay mucho más complicados).
Primer caso: en el denominador nos ha quedado una sola raíz cuadrada. Por ejemplo, racionaliza la siguiente expresión:
Para eliminar la raíz del denominador lo único que haremos será multiplicar y dividir la expresión por la misma raíz que aparece en el denominador:
A continuación realizamos los productos. Notamos que en el denominador, al hacer el producto de las dos raíces, se eliminan al ser iguales.
Segundo caso: en el denominador tenemos un binomio en el que uno de los términos, o los dos, son raíces cuadradas. Por ejemplo, racionaliza la siguiente expresión:
Para eliminar la raíz del denominador, dado que en este caso tenemos una resta (podía ser una suma), no lo conseguiríamos multiplicando éste solo por una raíz, ya que por la propiedad distributiva quedaría con el producto con el otro término. En este caso debemos multiplicar y dividir por otro binomio. Este será el mismo binomio pero cambiando el signo central. Es decir si es una resta lo convertimos en una suma y si es una suma en una resta. Es lo que se denomina expresión conjugada.
A continuación realizamos los productos:
Observa que en el denominador hemos aplicado una identidad notable. De hecho, siempre ocurrirá lo mismo al multiplicar por la expresión conjugada tendremos una suma por una diferencia y obtendremos la diferencia de dos cuadrados. Esto nos garantiza que se eliminarán las raíces en el denominador incluso cuando hubieran dos raíces.
Tercer caso: en el denominador tenemos una raíz que no es cuadrada. Por ejemplo, racionaliza la siguiente expresión:
Ahora multiplicaremos y dividiremos otra vez por una sola raíz, pero ésta debe ser tal que al multiplicarla por la que tenemos en el denominador se eliminen. Esto se consigue si la raíz por la que multiplicamos tiene el mismo índice (en este caso el 5), y en el radicando la misma base en la potencia, pero un exponente tal que sumado al que ya tenemos nos de un resultado igual al del índice. Es decir, como tenemos 2 en el exponente, debemos colocar una potencia con 3 en el exponente, ya que 2+3=5 (nos da el índice). Esto nos garantizará que la raíz se elimine.
El primer caso que hemos explicado es, en realidad, un caso particular de éste último.
Observa ahora este vídeo:
Ahora podéis practicar en la web ematematics donde tenéis una tarea con el nombre Racionalización 01










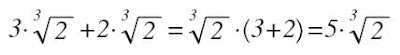


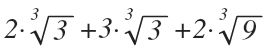
















No hay comentarios:
Publicar un comentario