Este es un tema de síntesis de todo lo estudiado durante este curso y anteriores. Aparecen conceptos de ecuaciones, inecuaciones, polinomios, trigonometría, geometría,...
Definición de función
Una función es una aplicación entre los elementos de dos conjuntos de forma que a cada elemento del conjunto inicial (al que llamaremos el conjunto de los originales) le corresponde como máximo un elemento del conjunto de llegada (al que llamaremos el conjunto de las imágenes).
Sería posible que una imagen tuviera más de un original, pero un original no puede tener 2 imágenes.
A los originales los denotamos por la letra x, y a las imágenes por la letra y. Decimos que x es una variable independiente (dado que podemos adjudicarle el valor que queramos) e y es una variable dependiente ya que tomará un determinado valor en función del que le hallamos dado a x.
Tanto el conjunto de salida como el de llegada pueden ser el conjunto de los números reales, en ese caso diremos que tenemos funciones reales (la y) de variable real (la x).
Al representar gráficamente la función lo que no ocurrirá es:
No puede ser que un original, en este caso x=-4, tenga más de una imagen, y en el ejemplo tiene 3, por lo que lo antes representado no es una función. (En realidad podría descomponerse en 3 funciones diferentes).
Formas de dar una función
Una función nos la pueden dar de 3 maneras diferentes: a través de una fórmula, a través de una tabla de valores, y a través de una gráfica.
La fórmula es la que muestra la relación que existe entre las dos variables, y suele ser una fórmula en la que tenemos la y despejada, por lo que decimos que y es función de x. y=f(x). A continuación vemos algunos ejemplos:
La tabla de valores nos muestra pares de valores de x e y dispuestos como sigue:
Una tabla es un método incompleto de dar una función, ya que solo tenemos un número finito de valores. Habitualmente la tabla la usamos para las rectas y para especificar los puntos singulares de otras funciones.
La tercera forma de dar la función es la representación gráfica. Éste será precisamente nuestro objetivo, hacer la gráfica de una función a partir de la fórmula. Sin embargo, también es recomendable saber interpretar una gráfica.
Dominio de una función
Ésta será la primera característica que estudiaremos de una función. El dominio de una función es el conjunto de todos los originales que tienen imagen. Es decir, no todos los valores posibles para x nos darán la posibilidad de hallar la y correspondiente. Veamos los diferentes casos.
Función polinómica. Para el caso de que la función tenga como fórmula un polinomio, el dominio será todo el conjunto de los números reales, ya que no existe ningún valor de x que no tenga la posibilidad de hallar su imagen. Por ejemplo, especifica el dominio de la siguiente función:
Por tratarse de una función polinómica, el dominio será todos los números reales.
Función racional. El dominio de una función que tenga polinomios en numerador y denominador, se buscará hallando los valores de x que anulan el denominador, ya que no es posible dividir entre 0. El dominio será todos los reales excepto los valores que anulan el denominador. A nivel práctico lo que tenemos que hacer es igualar el denominador a 0 y resolver la ecuación que se obtiene. Las soluciones de la ecuación son los valores que hay que excluir del dominio.
Por ejemplo, especifica el dominio de la siguiente función:
Lo que haremos será igualar el denominador a 0: x+2=0. Se resuelve la ecuación: x=-2. La solución de la ecuación es el valor que tengo que excluir del dominio. El dominio de esa función son todos los reales excepto el -2.
Función irracional. En el caso de las funciones que tengan raíces cuadradas no se podrá hallar la imagen cuando el interior de la raíz nos dé negativo. Así que lo que se tendrá que resolver en estos casos es una inecuación. Por ejemplo, halla el dominio de la siguiente función:
Para ello tenemos que resolver la siguiente inecuación: 3x-1>0. Se obtiene que x>1/3. El dominio por tanto serán todos los valores mayores o iguales a 1/3.
Existen muchos más casos, pero los iremos viendo en los siguientes temas. Ahora observa el siguiente vídeo:
Ahora es momento de practicar. En ematematicas tienes una tarea con el nombre de Dominio01.
Simetrías de la función
En este apartado estudiaremos algunas de las simetrías que puede tener una función. Estudiaremos únicamente las que se denominan simetría par e impar, dada su importancia, por ejemplo en física.
Simetría par. Una función tiene simetría par si al sustituir la x por -x la función recupera su forma inicial.
Por ejemplo:
En la función anterior cuando sustituyamos x por -x, al ser todos los exponentes pares el signo menos desaparece y vuelve a quedar la misma función.
Las funciones que tienen simetría par, al representarlas gráficamente observamos que son simétricas respecto del eje de las y. Por ejemplo, la función anterior queda en un gráfico:
Simetría impar. Una función tiene simetría impar si al sustituir x por -x la función queda igual pero con un signo menos delante de toda ella. Es decir, se puede sacar signo menos factor común y lo que queda dentro del paréntesis es la función inicial.
Por ejemplo:
Al sustituir x por -x, en el numerador queda un signo -, pero en el denominador no se modifica, así que ese signo - del numerador sale factor común:
Las funciones que tienen simetría impar, al representarlas gráficamente observamos que son simétricas respecto del origen de coordenadas. Es decir, si doblamos por el eje y, y a continuación por el eje x, las dos ramas de la función coincidirían.
La anterior función representada gráficamente sería:
Observa a continuación los siguientes vídeos:
Simetrías de la función
En este apartado estudiaremos algunas de las simetrías que puede tener una función. Estudiaremos únicamente las que se denominan simetría par e impar, dada su importancia, por ejemplo en física.
Simetría par. Una función tiene simetría par si al sustituir la x por -x la función recupera su forma inicial.
Por ejemplo:
En la función anterior cuando sustituyamos x por -x, al ser todos los exponentes pares el signo menos desaparece y vuelve a quedar la misma función.
Las funciones que tienen simetría par, al representarlas gráficamente observamos que son simétricas respecto del eje de las y. Por ejemplo, la función anterior queda en un gráfico:
Simetría impar. Una función tiene simetría impar si al sustituir x por -x la función queda igual pero con un signo menos delante de toda ella. Es decir, se puede sacar signo menos factor común y lo que queda dentro del paréntesis es la función inicial.
Por ejemplo:
Al sustituir x por -x, en el numerador queda un signo -, pero en el denominador no se modifica, así que ese signo - del numerador sale factor común:
Las funciones que tienen simetría impar, al representarlas gráficamente observamos que son simétricas respecto del origen de coordenadas. Es decir, si doblamos por el eje y, y a continuación por el eje x, las dos ramas de la función coincidirían.
La anterior función representada gráficamente sería:
Observa a continuación los siguientes vídeos:
Puntos de corte con los ejes
Como habíamos explicado en el apartado "formas de dar una función", es posible dar una función a partir de una tabla de valores, pero también es útil cuando queremos representar gráficamente una función a partir de su ecuación, hallar algunos puntos y escribirlos en una tabla de valores. Concretamente, los puntos que resultan más útiles, y a la vez más fáciles de hallar son los puntos de corte con los ejes, es decir cuando la x=0 (puntos de corte con el eje OY) y cuando la y=0 (punto de corte con el eje OX).
Veamos un ejemplo. Dada la función
halla los puntos de corte con los ejes.
Para ello lo que tenemos es que sustituir la x por 0 y hallar el correspondiente valor de y:
Es decir que para x=0 tenemos que y=-1.
A continuación sustituimos la y por 0 y hallamos el correspondiente valor de x.
En este caso ha habido que resolver una ecuación de segundo grado y se han obtenido dos valores. Así que para y=0 tenemos que x=3 y también x=-3.
Finalmente podemos disponer los tres puntos de corte obtenidos en una tabla de valores:
Esta tabla de valores puede ampliarse con puntos adicionales que nos ayuden a dibujar el gráfico, como veremos más adelante los extremos de la función.
En el siguiente vídeo se hallan los puntos de corte a partir de la representación gráfica de la función:
Discontinuidades de la función
Una función se dice que es continua si puede representarse gráficamente sin levantar el lápiz. No tiene huecos, agujeros, saltos o se va al infinito hacia arriba o hacia abajo. Todo lo anterior son discontinuidades, por lo que deben clasificarse. La clasificación de las discontinuidades que vamos a hacer será lo más sencilla posible por lo que solo hablaremos de tres tipos (aunque se puede complicar): discontinuidad evitable, discontinuidad asintótica y discontinuidad de salto.
Discontinuidad evitable. Esta discontinuidad aparece cuando la gráfica tiene un agujero en un punto. Es decir, únicamente para un valor de x que no puede hallarse el valor de y y tenemos que dejar un agujero en ese punto.
Pongamos un ejemplo. Halla las discontinuidades de la siguiente función:
Para esta función, si buscamos su dominio será:
Discontinuidad evitable. Esta discontinuidad aparece cuando la gráfica tiene un agujero en un punto. Es decir, únicamente para un valor de x que no puede hallarse el valor de y y tenemos que dejar un agujero en ese punto.
Pongamos un ejemplo. Halla las discontinuidades de la siguiente función:
Para esta función, si buscamos su dominio será:
En x=-3 no podemos hallar la y (no existe su valor), pero tenemos que saber si es porque hay un agujero (una discontinuidad evitable). Para ello lo que se hace es calcular el límite de la función cuando la x tiende a -3. El límite de una función en un punto es un concepto matemático que, para no tener que explicarlo a través de la definición, se puede explicar viendo a qué valor se acerca la y a medida que los valores de x se van acercando a -3. El límite no calcula el valor en ese punto, si no es una tendencia.
Sin embargo, calcular un límite es bastante sencillo, pues también se halla sustituyendo la x por el valor al que tiende. Sigamos con el ejemplo:
En este caso hemos llegado a una expresión curiosa 0/0. Decimos que una expresión de este tipo, dentro del cálculo con límites, es una indeterminación. Las indeterminaciones son expresiones que indican que todavía no hemos llegado a resolver el límite (está indeterminada su solución). Se trata de callejones sin salida por lo que debemos retomar la ecuación inicial y operarla de tal manera que nos sea posible resolver el límite. En el caso que nos ocupa, este tipo de indeterminación puede resolverse si previamente descomponemos factorialmente los polinomios y simplificamos los factores comunes en numerador y denominador. A continuación volvemos a calcular el límite y veremos que ya entonces obtendremos un resultado.
Importante: debemos seguir poniendo el límite en todos los pasos hasta que no se halla calculado.
En los casos en que tras hallar el valor del límite en los puntos que no pertenecían al dominio éste tenga un valor numérico (diferente de infinito) en esos puntos (en este caso en x=-3) existen discontinuidades evitables, es decir, agujeros. Al realizar la representación gráfica dibujaremos un pequeño círculo vacío que nos informará del agujero.
Curiosamente, la función del ejemplo al representarla tiene la gráfica de una recta, concretamente de y=x-3, excepto en x=-3 donde tendrá un agujero.
Discontinuidad asintótica. Asíntotas verticales
El siguiente caso de discontinuidad que vamos a estudiar es aquel que, a medida que nos acercamos al valor de x que no pertenecía al dominio, las y se van haciendo muy grandes o muy pequeñas (tienden a infinito). Vamos a verlo con un ejemplo. Halla las discontinuidades de la siguiente función:
Para ello primero buscaremos el dominio de la función:
Es en x=-1 donde la función tiene una discontinuidad. Para saber de qué tipo es hacemos el límite para x tendiendo a -1 y comprobamos hacia dónde se dirige la función (la y).
Ésta es la diferencia fundamental entre buscar una imagen (un valor de la función, de la y) y buscar un límite. En el caso del límite sí que es posible hallar un resultado cuando tenemos 0 en el denominador, y ese resultado decimos que es infinito (sin entrar en discusión acerca del signo). Podemos decir que el límite es infinito ya que es una tendencia, la función tiende a infinito.
En estos casos decimos que la función tiene en ese punto una discontinuidad asintótica, y que por tanto presenta una asíntota vertical. La asíntota vertical es una recta vertical hacia la que la función se dirige a medida que nos acercamos a la x por donde pasa la asíntota pero que no llega a tocarla nunca (la tocaría en el infinito si pudiera alcanzarlo). La ecuación de la asíntota vertical es x=-1.
Por último tenemos las discontinuidades de salto, pero que estudiaremos en un apartado posterior: funciones definidas a trozos.
Asíntotas horizontales y oblicuas
A continuación estudiaremos el comportamiento de la función a medida que las x se hacen cada vez más grandes (o más pequeñas), es decir, a medida que las x tienden a infinito. A medida que nos vamos alejando del origen de coordenadas, la función puede crecer indefinidamente y dirigirse hacia el infinito, o bien puede no sobrepasar una recta que le hace de frontera (lo cual no quiere decir que no crezca también indefinidamente). Estas rectas que marcan una frontera a la función son lo que llamamos asíntotas horizontales y oblicuas. La forma de hallarlas es calculando el límite cuando las x tienden a infinito y ver hacia dónde se dirige la función.
Asíntota horizontal. La asíntota horizontal se busca haciendo el límite de la función cuando x tiende a infinito, y si el resultado es un número (incluido el 0), y igual a ese número será la ecuación de la asíntota horizontal.
Veamos un ejemplo. Halla la asíntota horizontal de la siguiente función:
Para ello hacemos el límite para x tendiendo a infinito:
Los límites cuando la x tiende a infinito se calculan de la misma manera, sustituyendo la x por infinito, pero ahora debemos saber calcular con infinitos. Los infinitos pueden ser sometidos a casi cualquier operación que seguirán siendo infinitos. Así que tanto en numerador como en denominador quedarán sendos infinitos.
Sin embargo, la división de dos infinitos es una vez más una indeterminación. Todavía no podemos asegurar cual será el resultado del límite. Para ello podemos proceder de la siguiente manera: dividimos todos los términos de la función por la parte literal de mayor grado. En nuestro caso el mayor grado es 1 y x es esa parte literal:
Asíntota oblicua. La asíntota horizontal es un caso particular de otro más general como es el de la asíntota oblicua. Una asíntota oblicua es una recta con pendiente diferente de cero (que sería el caso de la horizontal) a la que tiende la función cuando la x tiende a infinito. Generalmente buscaremos la asíntota oblicua en funciones racionales tales que el grado del polinomio del numerador sea solo una unidad mayor que el grado del polinomio del denominador. Pongamos un ejemplo. Halla la asíntota oblicua de la siguiente función:
Sin embargo, calcular un límite es bastante sencillo, pues también se halla sustituyendo la x por el valor al que tiende. Sigamos con el ejemplo:
En este caso hemos llegado a una expresión curiosa 0/0. Decimos que una expresión de este tipo, dentro del cálculo con límites, es una indeterminación. Las indeterminaciones son expresiones que indican que todavía no hemos llegado a resolver el límite (está indeterminada su solución). Se trata de callejones sin salida por lo que debemos retomar la ecuación inicial y operarla de tal manera que nos sea posible resolver el límite. En el caso que nos ocupa, este tipo de indeterminación puede resolverse si previamente descomponemos factorialmente los polinomios y simplificamos los factores comunes en numerador y denominador. A continuación volvemos a calcular el límite y veremos que ya entonces obtendremos un resultado.
Importante: debemos seguir poniendo el límite en todos los pasos hasta que no se halla calculado.
En los casos en que tras hallar el valor del límite en los puntos que no pertenecían al dominio éste tenga un valor numérico (diferente de infinito) en esos puntos (en este caso en x=-3) existen discontinuidades evitables, es decir, agujeros. Al realizar la representación gráfica dibujaremos un pequeño círculo vacío que nos informará del agujero.
Curiosamente, la función del ejemplo al representarla tiene la gráfica de una recta, concretamente de y=x-3, excepto en x=-3 donde tendrá un agujero.
Discontinuidad asintótica. Asíntotas verticales
El siguiente caso de discontinuidad que vamos a estudiar es aquel que, a medida que nos acercamos al valor de x que no pertenecía al dominio, las y se van haciendo muy grandes o muy pequeñas (tienden a infinito). Vamos a verlo con un ejemplo. Halla las discontinuidades de la siguiente función:
Para ello primero buscaremos el dominio de la función:
Es en x=-1 donde la función tiene una discontinuidad. Para saber de qué tipo es hacemos el límite para x tendiendo a -1 y comprobamos hacia dónde se dirige la función (la y).
Ésta es la diferencia fundamental entre buscar una imagen (un valor de la función, de la y) y buscar un límite. En el caso del límite sí que es posible hallar un resultado cuando tenemos 0 en el denominador, y ese resultado decimos que es infinito (sin entrar en discusión acerca del signo). Podemos decir que el límite es infinito ya que es una tendencia, la función tiende a infinito.
En estos casos decimos que la función tiene en ese punto una discontinuidad asintótica, y que por tanto presenta una asíntota vertical. La asíntota vertical es una recta vertical hacia la que la función se dirige a medida que nos acercamos a la x por donde pasa la asíntota pero que no llega a tocarla nunca (la tocaría en el infinito si pudiera alcanzarlo). La ecuación de la asíntota vertical es x=-1.
Por último tenemos las discontinuidades de salto, pero que estudiaremos en un apartado posterior: funciones definidas a trozos.
Asíntotas horizontales y oblicuas
A continuación estudiaremos el comportamiento de la función a medida que las x se hacen cada vez más grandes (o más pequeñas), es decir, a medida que las x tienden a infinito. A medida que nos vamos alejando del origen de coordenadas, la función puede crecer indefinidamente y dirigirse hacia el infinito, o bien puede no sobrepasar una recta que le hace de frontera (lo cual no quiere decir que no crezca también indefinidamente). Estas rectas que marcan una frontera a la función son lo que llamamos asíntotas horizontales y oblicuas. La forma de hallarlas es calculando el límite cuando las x tienden a infinito y ver hacia dónde se dirige la función.
Asíntota horizontal. La asíntota horizontal se busca haciendo el límite de la función cuando x tiende a infinito, y si el resultado es un número (incluido el 0), y igual a ese número será la ecuación de la asíntota horizontal.
Veamos un ejemplo. Halla la asíntota horizontal de la siguiente función:
Para ello hacemos el límite para x tendiendo a infinito:
Los límites cuando la x tiende a infinito se calculan de la misma manera, sustituyendo la x por infinito, pero ahora debemos saber calcular con infinitos. Los infinitos pueden ser sometidos a casi cualquier operación que seguirán siendo infinitos. Así que tanto en numerador como en denominador quedarán sendos infinitos.
Sin embargo, la división de dos infinitos es una vez más una indeterminación. Todavía no podemos asegurar cual será el resultado del límite. Para ello podemos proceder de la siguiente manera: dividimos todos los términos de la función por la parte literal de mayor grado. En nuestro caso el mayor grado es 1 y x es esa parte literal:
Dado que el límite nos da igual a 1, decimos que y=1 es la asíntota horizontal.
Observa el siguiente vídeo en el que se explica cómo calcular varios límites en el infinito:Asíntota oblicua. La asíntota horizontal es un caso particular de otro más general como es el de la asíntota oblicua. Una asíntota oblicua es una recta con pendiente diferente de cero (que sería el caso de la horizontal) a la que tiende la función cuando la x tiende a infinito. Generalmente buscaremos la asíntota oblicua en funciones racionales tales que el grado del polinomio del numerador sea solo una unidad mayor que el grado del polinomio del denominador. Pongamos un ejemplo. Halla la asíntota oblicua de la siguiente función:
Se puede buscar la A.O. haciendo uso de unas fórmulas, pero para no tener que memorizar tantas fórmulas es mejor utilizar un procedimiento. Éste consiste en hacer primero la división entre los polinomios y escribir el resultado de la división como: cociente+resto/divisor. Apliquémoslo al ejemplo:
Si a continuación calculamos el límite cuando x tiende a infinito, la parte de resto/divisor tiende a 0, por lo que la función y el cociente de esta división tienden de la misma forma cuando x tiende a infinito, es decir, el cociente se corresponde con la asíntota oblicua. En nuestro ejemplo la A.O. es:
Máximos y mínimos. Crecimiento y decrecimiento.
La última característica que estudiaremos sobre las funciones es su crecimiento y decrecimiento. Éste viene dado por la pendiente de la curva de la función en cada punto de la misma. Este concepto, el de la pendiente de una función en un punto, se corresponde en matemáticas, con el de la derivada de una función en un punto. Es decir, que el cálculo de la derivada de una función está relacionado con su pendiente, y la pendiente está relacionada con el crecimiento. Si la pendiente es positiva, la función crece de izquierda a derechas, y si la pendiente es negativa, la función decrece. Pero además, si la pendiente es 0 en un punto, en ese punto la función tiene un extremo relativo (también podría tener un punto de inflexión que no estudiaremos este año), es decir, un máximo o un mínimo local (también podríamos tener extremos absolutos).
Por lo tanto, si calculamos la derivada de una función y la igualamos a cero, hallaremos los extremos de la función (los puntos que tienen pendiente cero).
Pero, ¿cómo se calcula la derivada de una función? Es posible utilizar la definición de derivada, pero lo que utilizaremos nosotros es una tabla de derivadas que, como si fuera una receta, nos permitirá calcularla en diferentes casos.
Si a continuación calculamos el límite cuando x tiende a infinito, la parte de resto/divisor tiende a 0, por lo que la función y el cociente de esta división tienden de la misma forma cuando x tiende a infinito, es decir, el cociente se corresponde con la asíntota oblicua. En nuestro ejemplo la A.O. es:
Máximos y mínimos. Crecimiento y decrecimiento.
La última característica que estudiaremos sobre las funciones es su crecimiento y decrecimiento. Éste viene dado por la pendiente de la curva de la función en cada punto de la misma. Este concepto, el de la pendiente de una función en un punto, se corresponde en matemáticas, con el de la derivada de una función en un punto. Es decir, que el cálculo de la derivada de una función está relacionado con su pendiente, y la pendiente está relacionada con el crecimiento. Si la pendiente es positiva, la función crece de izquierda a derechas, y si la pendiente es negativa, la función decrece. Pero además, si la pendiente es 0 en un punto, en ese punto la función tiene un extremo relativo (también podría tener un punto de inflexión que no estudiaremos este año), es decir, un máximo o un mínimo local (también podríamos tener extremos absolutos).
Por lo tanto, si calculamos la derivada de una función y la igualamos a cero, hallaremos los extremos de la función (los puntos que tienen pendiente cero).
Pero, ¿cómo se calcula la derivada de una función? Es posible utilizar la definición de derivada, pero lo que utilizaremos nosotros es una tabla de derivadas que, como si fuera una receta, nos permitirá calcularla en diferentes casos.
Como se aprecia en la tabla, la derivada la indicamos con un apóstrofo.
Por ejemplo, si tuviéramos que calcular la derivada de la función del ejercicio de la asíntota oblicua,
el resultado sería:
Para realizar esta derivada hemos utilizado la regla del cociente, pero además la de la suma y la resta de funciones y la derivada de potencias y constantes. Una vez hallada la derivada se iguala a cero para hallar los extremos, obteniendo una ecuación cuyas soluciones se corresponderán con los candidatos a máximos y mínimos.
Una vez hallada la x, es necesario buscar su imagen correspondiente, ya que cuando queramos representar la función en un gráfico, necesitaremos saber dónde situar dichos puntos.
¿Cómo sabemos si son máximos o mínimos? Existen diferentes métodos (como la segunda derivada), pero nosotros utilizaremos una tabla en la que además averiguaremos los intervalos de crecimiento y decrecimiento de la función. Dicha tabla se construye colocando en el margen izquierdo los intervalos formados por los extremos y los puntos que no pertenecen al dominio, y los ordenaremos en orden creciente desde menos infinito a más infinito. Por otro lado, en el margen superior colocaremos el signo de la derivada y el consiguiente crecimiento o decrecimiento de la función. Cuando una función pase de crecer a decrecer en un punto, estaremos ante un máximo, y cuando pase de decrecer a crecer, estaremos ante un máximo.
En el siguiente vídeo se repasan algunos de los conceptos estudiados pero a partir de una gráfica definida a trozos ya representada. En el vídeo rango es lo mismo que recorrido de la función.











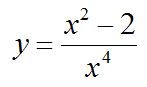














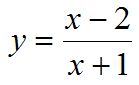













No hay comentarios:
Publicar un comentario