El tema de trigonometría estudia las relaciones entre los lados de los triángulos y con sus ángulos. Por ello primero se tienen que estudiar las medidas de los ángulos. Repasa los cálculos con ángulos realizados en 2º de ESO.
Ángulos.
Los ángulos se pueden medir en diferentes unidades: grados sexagesimales o bien en radianes.
La unidad del radián se define como el ángulo de un arco igual al radio.
¿Cuántos radianes caben en una circunferencia completa? Dado que el perímetro de la circunferencia es
Por ejemplo. ¿Cuantos grados mide 1 rad?
Por otro lado, en matemáticas no suelen interesarnos ángulos mayores que 360º. Un ángulo mayor que 360º es como si hubiéramos dado más de una vuelta. (Si lo que queremos es resolver triángulos, no tienen sentido estos ángulos). En el caso de que nos dieran un ángulo mayor de 360º, nosotros lo reduciremos a la primera vuelta. Para ello es posible ir restándole 360 hasta obtener un número menor que 360 y ése será el valor del ángulo en la primera vuelta. Por ejemplo. ¿Cual es el valor del ángulo en la primera vuelta de 1450º?
1450-360=1090; 1090-360=730; 730-360=370; 370-360=10º
Proceder de esta manera es lento si el número es muy grande. En esos casos resulta más rápido dividir el número que me hayan dado entre 360. Nos quedamos con la parte entera del cociente y el resto será el número que buscamos.
Hemos dado 4 vueltas completas y nos sobran 10º.
Circunferencia goniométrica.
Los ángulos normalmente los representaremos sobre una circunferencia de radio 1. Sobre esta circunferencia representaremos unos ejes coordenados donde el origen coincide con el centro de la circunferencia. Los ángulos se empezarán a medir desde el eje positivo de las "x" y en el sentido contrario a las agujas del reloj.
El hecho de escoger como radio igual a 1 constituye una ventaja que veremos enseguida. También los ejes nos dividen la circunferencia en 4 cuadrantes que a efectos prácticos resultan también útiles, como ya se verá. El primer cuadrante es el de los ángulos agudos, que serán los primeros que estudiaremos.
Razones trigonométricas de un ángulo agudo.
Los ángulos agudos son los comprendidos entre 0º y 90º y los situaremos en la circunferencia goniométrica en el primer cuadrante.
Una razón trigonométrica es una relación (cociente) entre dos lados de un triángulo. En el triángulo designaremos los ángulos por letras mayúsculas y los lados con minúsculas, escogiendo la misma letra para el lado opuesto al ángulo:
Se definen 3 razones trigonométricas básicas (también existen sus inversas) que son: seno, coseno y tangente. Sus definiciones para el ángulo B de la figura anterior son:
Siempre la razón va seguida de un ángulo, es la razón de un ángulo. No tiene sentido sen=... debería ser senA=...
Los ángulos agudos son los comprendidos entre 0º y 90º y los situaremos en la circunferencia goniométrica en el primer cuadrante.
Una razón trigonométrica es una relación (cociente) entre dos lados de un triángulo. En el triángulo designaremos los ángulos por letras mayúsculas y los lados con minúsculas, escogiendo la misma letra para el lado opuesto al ángulo:
Se definen 3 razones trigonométricas básicas (también existen sus inversas) que son: seno, coseno y tangente. Sus definiciones para el ángulo B de la figura anterior son:
Observa el siguiente vídeo para completar la explicación:
Vamos a resolver algún ejercicio sencillo. Dado el siguiente triángulo:
Practica ahora. En ematematicas.net tienes una tarea con el nombre razones trigonométricas ángulo agudo
Seguidamente incluiremos las razones trigonométricas en la circunferencia goniométrica. El siguiente vídeo os lo aclarará:
Razones trigonométricas de algunos ángulos agudos.
A continuación daremos los valores de las razones trigonométricas de algunos ángulos agudos.
Tal y como se expone en el vídeo las razones trigonométricas dentro de la circunferencia goniométrica son:
Empezaremos por los más sencillos. Para 0º vemos que si vamos haciendo el ángulo cada vez más pequeño, ocurren dos cosas, que el seno se va haciendo también más pequeño (se acerca a 0) y el coseno se hace más grande (se acerca a 1). En el límite en el que A sea 0 tendremos que sen0º=0 y cos0º=1. Y al revés, a medida que A crece y se acerca a 90º el seno se acerca a 1 y el coseno a 0. En el límite sen90º=1; cos90º=0
Observa el siguiente vídeo:
Las siguientes razones interesantes son las de 30º y 60º. En el siguiente vídeo se ve una de las posibles deducciones.
Las últimas razones que consideraremos son las de 45º. En el siguiente vídeo vemos una deducción de su valor:
Con todo lo visto se puede escribir una tabla con los resultados:
La anterior tabla es necesario sabérsela de memoria para poder resolver una serie de ejercicios sin utilizar la calculadora.
Relaciones fundamentales de la trigonometría.
Son muchas las relaciones que pueden establecerse entre las razones trigonométricas. La primera ya la hemos utilizado. Es la que relaciona las tres razones:
Su demostración es directa a partir de las definiciones de las razones:
Esta relación es muy útil para conocer la tangente a partir del seno y coseno.
La siguiente relación fundamental implica al seno y el coseno:
Esta relación se demuestra a partir del teorema de Pitágoras. Si nos fijamos de nuevo en la circunferencia goniométrica:
y aplicando el teorema de Pitágoras al triángulo dibujado en el interior de la circunferencia la relación se obtiene de forma inmediata.
Observa el siguiente vídeo si te ha quedado alguna duda:
Observa el siguiente vídeo si te ha quedado alguna duda:
Esta relación es útil para averiguar el seno si nos proporcionan el coseno o viceversa. Pondremos algún ejemplo: Dado sen 35=0,57 halla las demás razones trigonométricas.
Evidentemente se debe resolver utilizando las relaciones anteriores. Para ello sustituimos el valor del seno en la segunda fórmula fundamental y nos queda:
Ahora solo tenemos que despejar el cos 35º:
Para la tangente utilizamos la primera relación fundamental:
Evidentemente se debe resolver utilizando las relaciones anteriores. Para ello sustituimos el valor del seno en la segunda fórmula fundamental y nos queda:
Ahora sí que podemos usar la calculadora para comprobar los resultados. Vemos que cos35º=0,819... y que tg35º=0,7... La diferencia con nuestros resultados se deben a que el enunciado del ejercicio ya utilizaba un valor aproximado, así que nuestros resultados también son aproximados.
Otro ejercicio un poco más complicado es si de entrada nos dan la tangente. En ese caso debemos utilizar las dos relaciones conjuntamente como si resolviéramos un sistema. Sin embargo, puede resultar más útil utilizar la fórmula que se obtiene de realizar la siguiente operación. Si en la segunda relación dividimos todos los términos por el coseno al cuadrado se obtiene:
Simplificando y utilizando la primera relación:
La fórmula anterior ya nos permitiría hallar el coseno sabiendo la tangente. Luego para hallar el seno es posible usar cualquiera de las dos relaciones fundamentales.
También podemos relacionar el seno con la tangente si en lugar de dividir por el coseno al cuadrado, dividimos por el seno al cuadrado.
Vamos a poner algún ejemplo. Dada la tg57º=1,54 halla las demas razones trigonométricas.
Usaremos la primera fórmula que relaciona la tangente con el coseno para averiguar primero éste.
Ahora tenemos que despejar el coseno de 57:
Ahora el seno puede hallarse mediante cualquiera de las dos relaciones. Escojamos la primera:
Que si comprobamos con la calculadora veremos que en este caso nos coinciden los dos primeros decimales.
Razones trigonométricas para un ángulo cualquiera.
El siguiente paso es considerar ángulos que no necesariamente sean menores que 90º (es decir, ángulos que estén en el primer cuadrante), si no que consideraremos ángulos entre 0º y 360º.
En cada cuadrante podemos dibujar sobre la circunferencia goniométrica cómo quedarían los senos y los cosenos de la siguiente manera:
Otro ejercicio un poco más complicado es si de entrada nos dan la tangente. En ese caso debemos utilizar las dos relaciones conjuntamente como si resolviéramos un sistema. Sin embargo, puede resultar más útil utilizar la fórmula que se obtiene de realizar la siguiente operación. Si en la segunda relación dividimos todos los términos por el coseno al cuadrado se obtiene:
También podemos relacionar el seno con la tangente si en lugar de dividir por el coseno al cuadrado, dividimos por el seno al cuadrado.
Usaremos la primera fórmula que relaciona la tangente con el coseno para averiguar primero éste.
Razones trigonométricas para un ángulo cualquiera.
El siguiente paso es considerar ángulos que no necesariamente sean menores que 90º (es decir, ángulos que estén en el primer cuadrante), si no que consideraremos ángulos entre 0º y 360º.
En cada cuadrante podemos dibujar sobre la circunferencia goniométrica cómo quedarían los senos y los cosenos de la siguiente manera:
En esta web tienes una simulación java.
Como consecuencia de la orientación de cada uno de los segmentos que representan el seno y el coseno en cada cuadrante, éstos tienen signo positivo o negativo. Si el seno se orienta hacia arriba tiene signo positivo, si se orienta hacia abajo tiene signo negativo. El coseno si se orienta hacia la derecha tiene signo positivo, y si se orienta hacia la izquierda tiene signo negativo. En resumen se puede escribir que:
Ahora el ejercicio que habíamos resuelto para el primer cuadrante se complica ligeramente con la inclusión del signo correspondiente al cuadrante en el que se sitúe el ángulo.
Por ejemplo: Sabiendo que senA=-0,3 y que el ángulo pertenece al 4º cuadrante, halla las demás razones trigonométricas.
Procedemos como siempre, utilizando la segunda relación fundamental de la trigonometría, pero si os dais cuenta, esa fórmula tiene cuadrados. Al despejar un cuadrado y pasarlo al otro lado en forma de raíz cuadrada, habitualmente se le coloca delante un signo más menos. ¿Tiene sentido ese signo? Aquí sí, ya que existen dos ángulos que tienen el mismo seno. Para saber qué signo debemos poner necesitamos información adicional, esa información es la que nos indica en qué cuadrante se sitúa el ángulo.
Al principio hemos puesto el doble signo, pero luego, al aplicar las condiciones del ejercicio, y por situarse el ángulo en el 4º cuadrante, hemos dejado solo el signo + que es el que toma el coseno en ese cuadrante.
Para la tangente simplemente dividimos seno entre coseno y el signo aparece de forma natural:
A continuación puedes ver un vídeo en el que se resuelve un ejercicios similar pero usando varios métodos. El primero es el que hemos explicado.
Razones trigonométricas inversas.
Además de las razones estudiadas, tenemos para cada una de ellas la razón inversa. Es decir si en lugar de tener el seno tenemos 1 partido por el seno, entonces obtenemos una nueva razón cuya definición sería inversa a la del seno, es decir: hipotenusa entre cateto opuesto.
Éstas son las tres razones inversas, cosecante, secante y cotangente:
Con la introducción de estas razones podemos resolver ejercicios como: sabiendo que cosecA=1,3 y que el ángulo se encuentra en el 2º cuadrante halla el resto de razones.
Saber la cosecante implica conocer el seno directamente, basta hacer la inversa:
senA=1/cosecA=1/1,3=0,77.
A partir de aquí se procede como habíamos hecho en los ejercicios anteriores:
Para seguir practicando tienes una tarea en ematematicas con el nombre relación entre razones01
Reducción al primer cuadrante.
Conocidas las razones trigonométricas de algunos ángulos del primer cuadrante, es posible conocer las razones de los ángulos de otros cuadrantes por simple simetría. Empecemos viendo las razones del segundo cuadrante respecto al primero.
Como vemos en el dibujo anterior, los ángulos alfa y beta tienen, por simetría, el mismo seno (en verde), y el coseno (en azul) es también igual aunque de signo cambiado. Los ángulos que cumplen esta relación y que además suman 180º se denominan ángulos suplementarios.
Pongamos un ejemplo. Halla las razones trigonométricas de 135º.
Si situamos el ángulo de 135º vemos que se encuentra en el 2º cuadrante. También vemos que le faltan 45º para llegar a los 180º. Así que 45º y 135º son suplementarios por lo que tienen el mismo seno, y el coseno cambiado de signo.
Ángulos que difieren en 180º. Relación entre ángulos del tercer y primer cuadrante.
Estos ángulos, si los restamos, obtenemos un ángulo de 180º:
Como puede observarse en el dibujo, tienen seno y coseno iguales aunque cambiados ambos de signo.
Pongamos un ejemplo. Halla las razones trigonométricas de 225º.
El ángulo 225º se encuentra en el 3er cuadrante y difiere de 45º en 180º. Por lo tanto es con el de 45º con el que lo relacionamos.
Finalmente se puede establecer una relación entre las razones de ángulos del mismo primer cuadrante. Son ángulos que entre ellos suman 90º y que se denominan ángulos complementarios.
La particularidad de estos ángulos es que el seno de uno es igual al coseno del otro y viceversa.
Un ejemplo que ya hemos visto es el caso de 30º y 60º. sen30º=cos60º y cos30º=sen60º. Pero podemos pensar en muchos otros casos.
Puedes ahora ver el siguiente vídeo por si te ha quedado alguna duda.
El ángulo 225º se encuentra en el 3er cuadrante y difiere de 45º en 180º. Por lo tanto es con el de 45º con el que lo relacionamos.
La tangente obviamente será igual a 1.
Ángulos opuestos. Relación entre ángulos del cuarto y primer cuadrante.
Los ángulos opuestos son aquellos que suman 360º. Tienen el seno igual pero cambiado de signo y el coseno es el mismo.
Para el ángulo opuesto en ocasiones puede especificarse como el mismo cambiado de signo:
Pongamos un ejemplo. Halla las razones trigonométricas de 300º.
El ángulo junto con el que suma 360º es el de 60º. Así 300º y 60º son opuestos.
Puedes ahora ver el siguiente vídeo por si te ha quedado alguna duda.
Puedes practicar en ematematicas en la tarea: relación razones trigonométricas01
Resolución de triángulos.
Resolver un triángulo significa que, dados algunos datos del triángulo, hallar el resto de datos que desconocemos. Es decir, conociendo algunos de sus lados o ángulos, averigüemos el resto de ángulos y lados que desconocemos.
Como en el resto del tema, los triángulos que resolveremos en este curso son todos rectángulos. En caso de que en el problema no nos aparezcan inicialmente triángulos rectángulos, descompondremos las figuras para que finalmente aparezcan. (Por ejemplo, un triángulo isósceles puede descomponerse en dos rectángulos).
Dado el siguiente triángulo rectángulo:
las fórmulas que disponemos para resolver el triángulo son:
Teorema de Pitágoras:
La suma de los tres ángulos: A+B+C=180º
Y las definiciones de las razones trigonométricas:
También podríamos definirlas de forma análoga para el ángulo C.
Combinando las 5 fórmulas podemos resolver cualquier triángulo rectángulo del que conozcamos los datos necesarios.
Por ejemplo, dados C=45º y b=20 cm. halla el resto de lados y ángulos del triángulo rectángulo.
Sabiendo que es rectángulo, A=90º, por lo que B=180-90-45=45º.
Luego hallamos los lados:
Para el lado c podemos utilizar el teorema de Pitágoras o el cosB. Usando Pitágoras:
Como era de esperar, ya que se trata de un triángulo rectángulo isósceles.
Este tipo de ejercicios pueden aplicarse a la resolución de una gran cantidad de problemas de trigonometría. Veamos un ejemplo en el siguiente vídeo:
En ematematicas.net tenéis una tarea con el nombre: Resolución de triángulos rectángulos01 para practicar este apartado.
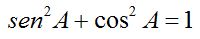
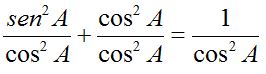
No hay comentarios:
Publicar un comentario