Sucesiones.
Una sucesión es una serie de números ordenados donde el orden es importante por ello cada uno de estos números queda ligado a un subíndice que indica su posición dentro de la sucesión. Es por ello que formalmente suelen definirse las sucesiones como una aplicación entre los números naturales (los subíndices) y los números reales (los términos de la sucesión). A cada natural le hacemos corresponder un real.
Los puntos suspensivos indican que, en principio, habrá infinitos términos (aunque también pueden definirse sucesiones finitas).
Las sucesiones pueden darse, como en el caso anterior, dando los primeros términos de la sucesión, pero también pueden darse mediante una fórmula que permita obtener cualquier término conociendo su posición. A esta fórmula se la conoce como término general o enésimo y solo depende de n (la posición). Existen sin embargo, otros tipos de sucesiones que en las que además debe darse el primer término, ya que son sucesiones en las que cada término depende de los anteriores. Se denominan sucesiones recurrentes y el ejemplo más famoso son los números de Fibonacci: 1,1,2,3,5,8,13,21,34,55,89... donde cada término es igual a la suma de los dos anteriores, pero debemos especificar también con qué número empezamos.
Existen muchos tipos de sucesiones más: convergentes, divergentes, monótonas, alternas...pero estudiaremos aquí dos tipos especialmente importantes, las que reciben el nombre de progresiones aritméticas y geométricas.
Si todavía tienes dudas o quieres profundizar en las sucesiones observa el siguiente vídeo:
Progresiones aritméticas.
Las progresiones aritméticas son aquellas en las que cada término se obtiene sumando una cantidad fija. A partir de un número inicial, le vamos sumando siempre lo mismo. Por ejemplo: 1,4,7,10,13,16,19... donde al primer término, en este caso 1, le sumamos siempre la misma cantidad, en este caso 3. Así 1+3=4; 4+3=7; 7+3=10 y así sucesivamente.
Término general de una progresión aritmética.
Lo primero que debemos hacer es saber reconocer cuando estamos ante una progresión aritmética. Las progresiones aritméticas se reconocen porque cada término se forma al sumar alguna cantidad constante al término precedente. Esa cantidad también podría ser negativa y en ese caso la progresión va decreciendo. Pongamos un ejemplo: 2,5,8,11,14... en este caso la cantidad que vamos sumando es 3. Para averiguar cuanto vale esa cantidad basta con restar el 2º termino menos el 1º: 5-2=3. Luego se comprueba que efectivamente el resto de términos se obtienen por adición del 3. Esa cantidad recibe entonces el nombre de diferencia, pues es la diferencia entre dos términos consecutivos de la progresión. Veamos otro ejemplo: 15, 10, 5, 0, -5... ahora la diferencia es: 10-15=-5 (es negativa).
A continuación vamos a deducir el término general o enésimo de la progresión aritmética. Es decir, una fórmula que me permitirá saber cualquier término sabiendo solo la posición que ocupa dentro de la progresión. Para ello vamos a escribir los primeros términos utilizando letras:
Como se puede ver, hemos colocado cada término, empezando por el primero con subíndice 1, y luego los siguientes y los hemos referido a los anteriores dejando siempre la expresión en función del primer término y de la diferencia d. Es evidente que el segundo término se obtiene sumando d al primero, y que el tercero se obtiene al haber sumado dos veces d al primero, y el cuarto al haber sumado 3d al primero y así sucesivamente hasta escribir el término enesimo (término general). Este término se escribirá, si seguimos la lógica del desarrollo como el primer término más un número de veces d. ¿Cuantas d tenemos que sumarle? Basta con fijarse que al 4º término le sumamos 3, al 5º cuatro, etc. Por lo tanto al término n le deberemos sumar n-1 veces d (una menos que la posición que ocupa, si ocupa la posición n, una menos será n-1). Así el término general de la progresión aritmética será:
Según vemos, para poder escribir el término general o enésimo basta con saber el primer término y la diferencia (n no debe sustituirse por ningún valor, es la variable, juega el mismo papel que la x de una ecuación) Por ejemplo, escribe el término general de la siguiente progresión: 3,5,7,9,11...
Lo primero será cerciorarse de que se trata de una progresión aritmética. Para ello restamos los términos consecutivos: 5-3=2; 7-5=2; 9-7=2... Así no solo hemos comprobado que se trata de una P.A. (progresión aritmética) si no que también hemos encontrado la diferencia: d=2. Ahora solo queda fijarse en el valor del primer término que es 3. Sabiendo la diferencia (2) y el primer término (3) ya puedo escribir el término general:
A partir de aquí lo que sí que podemos hacer es operar para dejar la expresión un poco más compacta:
Como se puede observar, en el término general sigue apareciendo la n. Ahora si quieres comprobar que lo has hecho bien solo tienes que sustituir la n por 1 y calcular el resultado (valor numérico de un polinomio) y verás que obtienes: 2·1+1=3 el primer término, si sustituyes la n por 2: 2·2+1=5, que es el 2º término, y así sucesivamente, con lo que habremos comprobado que la fórmula es la correcta.
Suma de n términos de una progresión aritmética.
Uno de los ejercicios más sencillos dentro de las progresiones aritméticas es el de sumar una cantidad de términos consecutivos de la progresión. Por ejemplo, si me piden sumar los 5 primeros términos de esta progresión: 2,4,6,8,10... al ser muy pocos lo puedo hacer directamente: 2+4+6+8+10=30, pero si en lugar de pedirme solo 5 términos me pidieran 100 o 1000, tardaría mucho tiempo sumándolos uno a uno. Debemos encontrar un método más rápido y directo. Para ello uno debe darse cuenta que si sumamos el primer término y el último de los que queremos incluir en la suma, por ejemplo en el caso sencillo de antes: 2+10=12, nos da lo mismo que si sumamos el segundo término y el penúltimo: 4+8=12; también nos daría lo mismo que sumar el tercero y el antepenúltimo (en este caso ya son el mismo): 6+6=12. Esta propiedad de las P.A. (bastante lógica por otro lado ya que cada vez sumamos y restamos la misma cantidad por lo que la suma se quedará igual) nos servirá para realizar la suma de forma más rápida. Si te fijas si a cada término le sumamos el que con él nos dará ese valor constante, en este caso el 12, obtendremos 5 veces el 12. Es decir: (2+10)+(4+8)+(6+6)+(8+4)+(10+2)=60. Si te fijas hemos obtenido justo el doble de lo que buscábamos por lo que ahora solo tendremos que dividir entre 2. 60:2=30 y ya tenemos la suma que buscábamos. ¿Qué hemos hecho? En realidad se resume en sumar el primer y último término, multiplicar esa suma por el número de términos que estamos sumando y dividirlo entre 2. Expresado como una fórmula esto es:
En esta ocasión n representa el número de términos que estamos sumando, por lo que ahora sí que se sustituirá por un valor. De hecho lo que buscamos aquí no es una fórmula, si no un número. Pongamos un ejemplo. Suma los 100 primeros números pares.
Este ejercicio es la continuación del ejemplo planteado. Ahora no sumaremos los 5 primeros términos, si no 100. Para ello es necesario saber cual es el término que ocupa la posición 100. Es evidente que éste es el 200, ya que en los primeros 200 naturales hay 100 pares y 100 impares, pero si queremos comprobarlo podemos usar la fórmula del término enésimo para las P.A.
Una vez conocido el último término podemos usar ya la fórmula de la suma de n términos:
Observa ahora el siguiente vídeo:
Progresiones geométricas.
Una progresión geométrica es aquella que se obtiene multiplicando cada término por una cantidad fija. Por ejemplo: 2,6,18,54,162,486... En este caso la cantidad fija que multiplica cada término para obtener el siguiente es 3.
¿Cómo reconocer una progresión geométrica (P.G.)? Basta con dividir el 2º término entre el 1º. El resultado de esa división será la cantidad por la que se van multiplicando todos los términos y recibe el nombre de razón de la P.G.
Término general de una progresión geométrica.
Vamos a deducir el término general o n-ésimo de una P.G. Para ello seguiremos los mismos pasos que en el caso de la P.A. Escribiremos los primeros términos y los dejaremos en función del primer término y de la razón, y a continuación deduciremos cual podría ser el término general.
En esta ocasión hemos ido un poco más rápido pues ya tenemos la experiencia de la P.A.
Pongamos un ejemplo, halla el término general de la siguiente sucesión: 1,3,9,27,81...
Lo primero es confirmar que se trata de una P.G. Si dividimos el 2º término entre el 1º obtenemos la razón: 3/1=3. También confirmamos que el resto de términos cumplen la misma relación: 9/3=3; 27/9=3; 81/27=3...
Una vez que sabemos que se trata de una P.G. y teniendo también la razón (r=3) basta con fijarse en el primer término (1) y sustituirlo todo en el término general:
Después lo que hemos hecho es operar la expresión para dejarla un poco más sencilla. Para ello lo que hacemos es escribir la potencia separando los exponentes utilizando la propiedad de las potencias (producto de potencias de la misma base sumamos los exponentes y dejamos la base). Luego pasamos la potencia de exponente negativo al denominador y queda positiva.
Observa a continuación el siguiente vídeo:
Vamos a deducir la suma de n términos de una P.G. Si escribimos la suma de n términos:
Utilizaremos el siguiente truco para deducir la fórmula. Primero multiplicaremos por la razón (r) en ambos miembros de la igualdad:
Seguidamente podemos ver que al multiplicar cada término por r se convierte en el siguiente y así lo escribiremos excepto en el último:
Seguidamente realizamos la resta entre ambas igualdades, la de la suma y la de la suma tras multiplicar por r:
En los segundos miembros se cancelarían todos los términos iguales quedando únicamente los dos que hemos escrito. A continuación solo tenemos que despejar Sn para obtener la fórmula de la suma de n términos de una P.G. Para ello sacamos Sn factor común y luego pasamos dividiendo la resta de r-1 al otro miembro:
También podemos dejar la fórmula en función solo del primer término, de la razón y del número de términos a sumar. Para ello introducimos la fórmula del término general:
No es necesario saber ambas fórmulas, con una es suficiente si se sabe pasar de una a otra.
Pongamos un ejemplo. Suma los 20 primeros términos de la siguiente progresión: 2,4,8,16,32...
Como siempre antes debe comprobarse qué tipo de progresión es. 4/2=8/4=16/8=32/16=...=2=r Si usamos la segunda fórmula basta con saber además el primer término (2) y el número de términos a sumar (20). Sustituyendo todos los valores en la fórmula se obtiene:
Suma de infinitos términos de una progresión geométrica.
Podríamos pensar que siempre que sumamos infinitos términos la suma se nos haga infinita, pero no siempre ocurrirá así. Si cada vez que sumamos un término éste es más pequeño que el anterior la suma no crece indefinidamente si no que se va acercando a un valor finito. Esto ocurre cuando la razón es un número entre 0 y 1.
Vamos a deducir la fórmula de la suma de infinitos términos de una P.G. Partimos de la fórmula de la suma de n términos y seguidamente sustituimos la n por infinito.
Ahora solo tenemos que averiguar qué significa la r elevada a infinito. Aunque todavía no has estudiado los límites, se ve fácilmente que si r es menor que 1, por ejemplo 0,5, cuando multipliques 0,5·0,5·0,5...hasta el infinito, como que cada vez se van obteniendo números más próximos a cero, en el infinito llegaríamos a cero (si es que se pudiera llegar a infinito, de ahí que hablemos de límites). Sustituyendo entonces la r elevada a infinito por cero y pasando el signo menos al denominador se obtiene:
Apliquemoslo a un ejemplo. Averigua la suma de todos los términos de la siguiente progresión: 1, 1/2, 1/4, 1/16, 1/32...
Lo primero que tenemos que comprobar (además de que sea una P.G.) es que la razón sea menor que 1. Efectivamente es 1/2. Ahora solo tenemos que aplicar la fórmula:
Si escribimos los primeros términos en forma decimal y vamos calculando las sumas parciales podemos entender porque la suma no se hace infinita y en este caso que tienda a 2.
1; 1+0,5=1,5; 1+0,5+0,25=1,75; 1+0,5+0,25+0,125=1,875; 1+0,5+0,25+0,125+0,0625=1,9375; 1,9375+0,03125=1,96875...
Observa ahora este vídeo:
Producto de n términos de una progresión geométrica
En este caso ocurre lo mismo que con la suma de los términos de una progresión aritmética, que el producto de los extremos de una progresión de n términos es igual que el producto del segundo término por el penúltimo, y así sucesivamente.
Pongamos un ejemplo: 2, 6, 18, 54, 162, 486 Se trata de una progresión geométrica de razón 3 (cada término se obtiene de multiplicar el anterior por 3). Si multiplicamos los extremos: 2·486=972; pero también: 6·162=972 y 18·54=972. Lo cual es completamente lógico y predecible, ya que todos los términos equidistantes se obtienen multiplicando y dividiendo por el mismo número, con lo que el resultado no se ve alterado.
Así que nos valdremos de esta propiedad para calcular el producto de n términos de la progresión. Como vemos en el ejemplo, lo que tendremos que multiplicar será 972·972·972, es decir, 972 al cubo. Pero para obtener una fórmula que me permita encontrar este producto más rápido vamos a disponer los números de la siguiente manera:
A continuación haremos el producto de ambas igualdades, por un lado me quedará el cuadrado de P6 y por otro los productos antes mencionados 2·486, 6·162...pero duplicados, es decir 6 veces el 972.
Es decir:
Despejando finalmente el P6 se obtiene:
Es decir, que el producto de 6 términos de una progresión geométrica se obtiene al hacer la raíz cuadrada del producto del primer término por el último y elevado ese producto al número de términos que estamos multiplicando. Esto escrito mediante una fórmula general es:
El caso es que este producto enseguida aumenta mucho a pocos términos que multipliquemos. Veamos otro ejemplo. Realiza el producto de los 10 primeros términos de la siguiente progresión geométrica: 1,4,16,64...
Dada la fórmula, vemos que lo primero que tendremos que averiguar es el término que ocupa la posición 10, es decir, el último de los que vamos a multiplicar. Para ello tenemos dos opciones: buscar todos los términos multiplicando sucesivamente por la razón hasta llegar al último término (el décimo en este caso), o bien utilizar el término general, lo que resulta más inteligente.
Ahora ya podemos aplicar la fórmula del producto:
Como hemos comentado antes, los productos crecen rápidamente y si calculamos el valor de esa potencia obtendremos:
Progresiones de segundo grado.
Una progresión de segundo grado tiene como término general:
Los coeficientes a, b y c son los que determinan una sucesión en particular. Por ejemplo si a=2, b=1 y c=-1 tendríamos:
Esta sucesión tendría como primeros términos:
Dados los primeros términos puede resultar un poco difícil hallar el término general. Lo primero, pero, sería saber que los primeros términos tienen como fórmula general una sucesión de segundo grado. Si restamos los términos sucesivos se obtiene 7, 11, 15, 19...que si se vuelven a restar se obtiene 4,4,4...(el mismo número) lo que nos indica que se trata de una sucesión de segundo grado. Cuando la segunda diferencia de los términos de una sucesión es una constante la sucesión es de segundo grado.
Para averiguar el término general utilizaremos el siguiente método. Daremos a "n" los valores n=1, n=2 y n=3 en la fórmula general y con ello obtendremos 3 ecuaciones con 3 incógnitas (es decir, un sistema de ecuaciones).
Los miembros de la derecha siempre serán los mismos, mientras que los de la izquierda se corresponden con los 3 primeros términos de la sucesión.
A continuación pasamos a resolver el sistema. La mejor forma es utilizar el método de reducción. Podemos restar la 2ª menos la 1ª y la 3ª menos la 2ª. Con ello se obtiene:
Seguidamente restamos la 1ª a la 2ª: 4=2a; a=2. El resto de incógnitas las obtenemos por sustitución. Tomando la 1ª ecuación del sistema anterior y sustituyendo el valor de a, se obtiene para b:
7=3·2+b
7-6=b
b=1
Conocidas a=2 y b=1 pasamos a hallar c de la primera ecuación: 2=2+1+c; c=-1. Una vez hallados los valores de a,b y c los sustituimos en la fórmula general obteniendo:
El siguiente vídeo muestra un par de ejemplos pero que se resuelven a golpe de imaginación (como dice en el vídeo, más imaginación que Julio Verne), pero el método que acabo de explicar, aunque un poco elaborado, es más seguro que nos llevará a la solución. Ponlo en práctica con los ejemplos del vídeo donde también verás la solución.
Interés compuesto
En el tema anterior ya vimos el interés simple, y en este tema vamos a estudiar el interés compuesto. La diferencia entre ambos tipos de interés es que en el compuesto, cada vez que completamos un año, los intereses se suman a nuestro capital de forma que al año siguiente calculamos los nuevos intereses teniendo en cuenta esa cantidad de más, cosa que no ocurría con el interés simple, donde siempre se calculaban los intereses con el mismo capital inicial.
Obviamente, el interés compuesto nos arrojará un resultado final mayor que en el interés simple.
Vamos a deducir la fórmula para este tipo de interés.
Supongamos que ingresamos un capital inicial de 1000€ durante un año a un rédito del 2%. Esto nos dará al cabo de un año un interés de 1000·2/100=20€. Estos 20€ se los sumamos al capital inicial para obtener el capital al primer año: 1000+20=1020€.
Para calcular los intereses del segundo año utilizamos esta cantidad: 1020 (y no la cantidad inicial: 1000 como haríamos con el interés simple). Así que para el segundo año ya calculando el total:
Al reiterar los pasos vemos que siempre es posible ir sacando factor común el 1+2/100=1+0,02=1,02
Es decir que se trata de una progresión geométrica de razón 0,02 y término inicial 1000 (por eso se estudia en este tema).
Siguiendo con nuestro ejemplo, vemos que el siguiente año (tercer año) tendremos:
Y, en general, en el año n tendremos:
De aquí se puede extrapolar fácilmente a una fórmula general:
Donde C es el capital final (incluidos los intereses); Ci es el capital ingresado inicialmente; r es el rédito anual en % (el partido por 100 es parte de este porcentaje); y n es el tiempo en años.
Por ejemplo, ¿Cuanto habremos cobrado de intereses a un interés compuesto del 0,2% durante 10 años si inicialmente ingresamos 5000€?
Primero con la fórmula anterior calcularemos el capital final:
Por ejemplo, ¿Cuanto habremos cobrado de intereses a un interés compuesto del 0,2% durante 10 años si inicialmente ingresamos 5000€?
Primero con la fórmula anterior calcularemos el capital final:
Ahora tenemos que hacer la diferencia entre el capital final e inicial para saber los intereses que nos han dado y éstos son: 100,90 €.
Observa ahora este vídeo para acabar de entender los dos tipos de interés estudiados.




































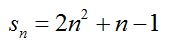






2 comentarios:
Aquí pueden encontrar ejercicios resueltos de progresiones aritméticas y geométricas.
Espero que les sirva de ayuda, un saludo!
Muchas gracias. Por supuesto que será una ayuda.
Un saludo
Publicar un comentario